抱歉，您的浏览器无法访问本站

本页面需要浏览器支持（启用）JavaScript


了解详情 >

cutlass layout algebra

请设置文章作者

发布于：Aug 29, 2025
次浏览

cutlass layout algebra: cheatsheet

约定:

  1. 永远都是一维index的映射/变换, 只不过可以构造一些逻辑上的view/layout
    • 逻辑空间: domain, 物理空间: co-domain
    • 所以index的范围是相同的
  2. column-major构建index
    • layout[idx] = column-major地walk一个shape
    • 对于一个shape=[a,b,c], walk顺序为: abc，而不是cba
  • Tips
    • column-major
    • 自动coalesce导致变化难理解

Terms

  • mode
    • 一个mode表示一个(rank)的(shape:stride)的表示: s0:d0
  • mn-layout
  • tv-layout
    • (tid, vid) -> 1d index的映射

indexing(Layout)

https://leimao.github.io/blog/CuTe-Index-To-Coordinate/

  • crd2idx(crd, layout)
    • 把一个坐标变成index
  • idx2crd(idx, layout)
    • 把一个index变成坐标
  • layout
    • 把一个index(N维index)变成另一个index

layout

column-major

把一个index(N维index)变成另一个index

计算方法:

  • Layout = (Mode0, Mode1, ... ModeN):(Stride0, Stride1, ... StrideN)
  • idx的坐标: Crd = (idx%Mode0, (idx/Mode0)%Mode1, ... , idx/(Mode0*Mode1*...*ModeN-1))
    • idx2crd
    • (c0, c1, ... cN):(Stride0, Stride1, ... StrideN)
  • 变化后的idx:
    • idx_new = c0*Stride0 + c1*Stride1 + ... + cN*StrideN
1
2
3
4
5
auto L = make_layout(make_shape(2, 4), make_stride(2, 2));
for (int i = 0; i < 8; i++) {
    print(L(i));
    print("\n");
}

输出

1
2
3
4
5
6
7
8
0
2
2
4
4
6
6
8

tv-layout

https://veitner.bearblog.dev/thread-value-layouts-in-cute/

tv_layout
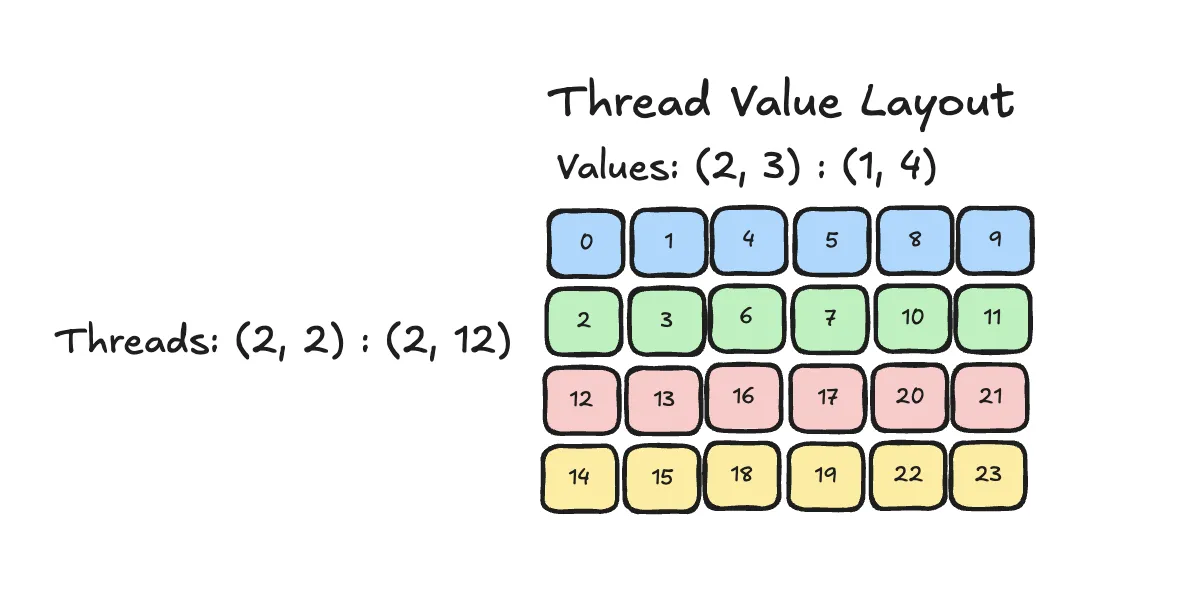
  • NOTE1
    • (tid, vid) - tv_layout -> idx
    • tid经过t_layout可以拿到thread的index
    • vid经过v_layout可以拿到thread内的value index
  • NOTE: 2
    • 如果单独抽出tv_layout的单个mode, 就能得到t_layout和v_layout
    • e.g. tv_layout: ((2, 2), (2, 3)):((2, 12), (1, 4)))
    • t_layout: (2, 2):(2, 12)
    • v_layout: (2, 3):(1, 4)

MMA Trait

注意几个混淆

  1. MMA_Traits中的A/B/CLayout是tv layout: (tid, vid) -> (m, n)
  2. mma图中的示意的layout不是tv layout, 而是(m, n) -> (tid, vid)的layout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
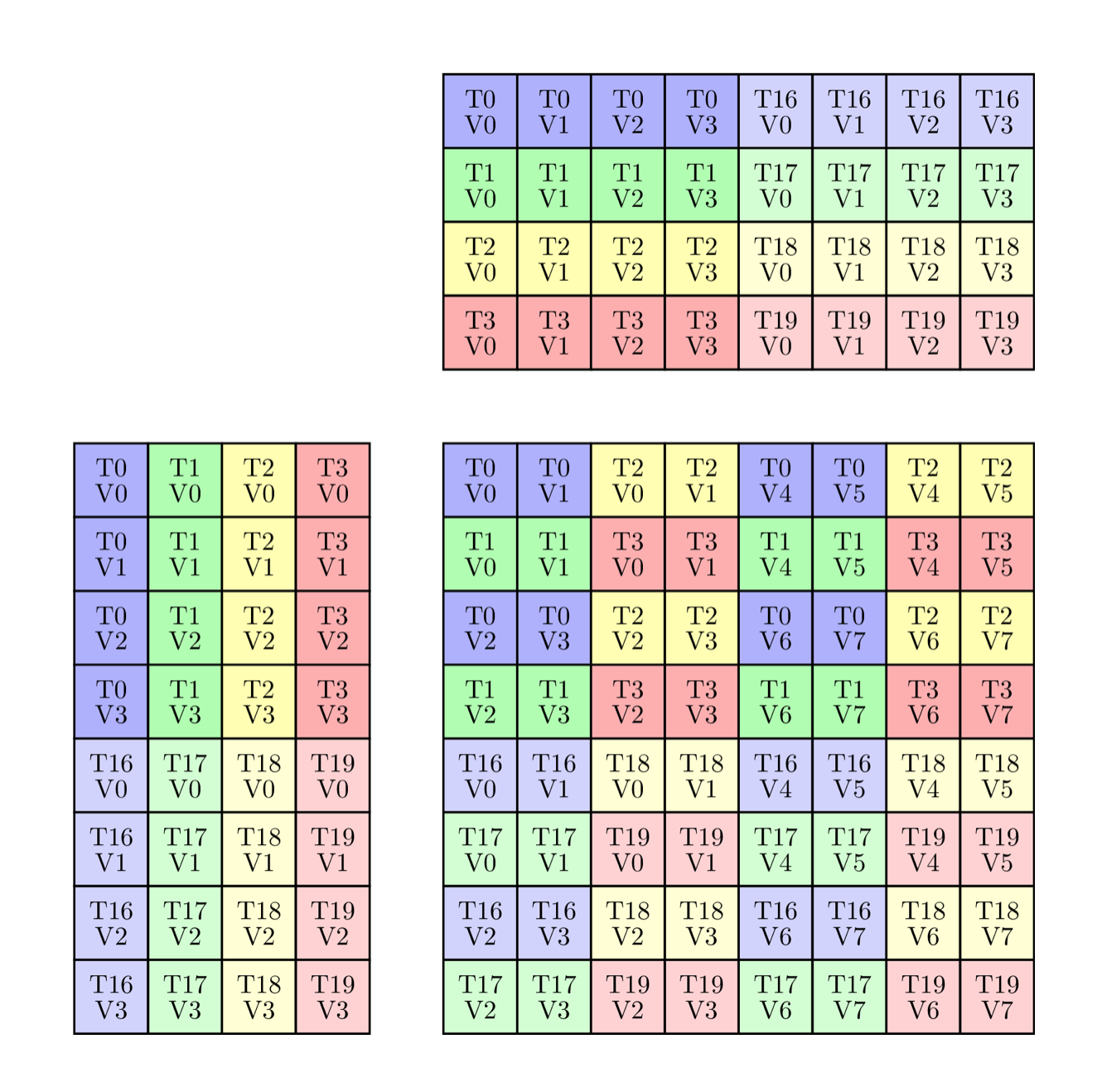
25
template <>
struct MMA_Traits<SM70_8x8x4_F32F16F16F32_NT>
{
    using ElementDVal = float;
    using ElementAVal = half_t;
    using ElementBVal = half_t;
    using ElementCVal = float;

    using Shape_MNK = Shape<_8,_8,_4>;

    using ThrID = Layout<Shape <_4, _2>,
    Stride<_1,_16>>;

    // (T8,V4) -> (M8,K4)
    using ALayout = Layout<Shape <Shape <_4,_2>,_4>,
    Stride<Stride<_8,_4>,_1>>;

    // (T8,V4) -> (N8,K4)
    using BLayout = Layout<Shape <Shape <_4,_2>,_4>,
    Stride<Stride<_8,_4>,_1>>;

    // (T8,V8) -> (M8,N8)
    using CLayout = Layout<Shape <Shape <_2, _2,_2>,Shape <_2,_2, _2>>,
    Stride<Stride<_1,_16,_4>,Stride<_8,_2,_32>>>;
};

如何计算tv layout

如下mma为例, 规定ALayout是(M,K)的column-major, BLayout是(N,K)的column-major。

不过示意图中的BLayout是(K,N)的, 所以如果要和图中对应, 需要把BLayout看成(N,K)的row-major。

  1. tv layout总是(tid, vid)的逻辑index, 同样的column major
  2. 观察thread数和value数, 得到tv layout的shape
  3. vid不变, step tid。观察物理index的变化, 得出tid的stride
    • 逻辑tid: [0..8], 至于图中是[0,1,2,3] [16,17,18,19]的应该ThrID映射的
    • (T0,V0) -> 0
    • (T1,V0) -> 8
    • (T2,V0) -> 16
    • (T3,V0) -> 24
    • (T4,V0) -> 4
    • ...
    • 所以t layout为: (4, 2):(8, 4)
  4. tid不变, step vid。观察物理index的变化, 得出vid的stride
    • (T0,V0) -> 0
    • (T0,V1) -> 1
    • (T0,V2) -> 2
    • (T0,V3) -> 3
    • 所以v layout为: (4):(1)
  5. t layout和v layout合并
    • tv layout得: ((4, 2), 4):((8, 4), 1)

inverse

求逆, 左逆, 右逆

TLDR

求倒排索引, 新索引的顺序根据老索引的value来排序

  1. 存在一一对应关系: X <-> Y
  2. X的范围和Y的范围相同 e.g. X是0到N-1, Y也是0到N-1
  3. 求逆: Y排序成X的样子, 然后对应的Y<->X的映射关系
  4. map[X] = Y, 从左值到右值成为左逆, 否则右逆

formula

  • let f: X->Y, g: Y->X
  • 称g是f的左逆, f是g的右逆

impl

naive:

1
2
3
4
5
6
index = [
    (0, 2),
    (1, 0),
    (2, 1)
]
inverse_index = sorted(index, key=lambda x: x[1])

cutlass:

TODO:

Coalesce

简化layout

TLDR

  • tips
    • mode删除: shape1不贡献stride, 其stride可以被忽略
    • mode合并: stride是连续的, 可以合并
  • s0:d0 ++ s1:d1 => Coalesce((s0, s1):(d0, d1))
  • s0:d0 ++ _1:d1 => s0:d0. Ignore modes with size static-1.
    • shape1不贡献stride, 这个mode可以被忽略
  • _1:d0 ++ s1:d1 => s1:d1. Ignore modes with size static-1.
    • shape1不贡献stride, 这个mode可以被忽略
  • s0:d0 ++ s1:s0d0 => s0s1:d0. If the second mode’s stride is the product of the first mode’s size and stride, then they can be combined.
    • 地址是连续的, 可以合并
  • s0:d0 ++ s1:d1 => (s0,s1):(d0,d1). Else, nothing can be done and they must be treated separately.
    • 无法合并, 只能保持原样

Composition

TLDR

  1. 假设有两个逻辑layout: A, B
    • R(c) := (A o B)(c) := A(B(c))
  2. 逻辑layout只能接受coordinate, 不能接受index
  3. 所以传递时总是idx2coor, 再传入layout得到一个新的idx
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Functional composition, R := A o B
R(c) := (A o B)(c) := A(B(c))

Example
A = (6,2):(8,2)
B = (4,3):(3,1)

**idx = column-major得walk shape**

        idx=input   idx2crd    idx=B   crd2idx
R( 0) = A(B( 0)) = A(B(0,0)) = A( 0) = A(0,0) =  0
R( 1) = A(B( 1)) = A(B(1,0)) = A( 3) = A(3,0) = 24
R( 2) = A(B( 2)) = A(B(2,0)) = A( 6) = A(0,1) =  2
R( 3) = A(B( 3)) = A(B(3,0)) = A( 9) = A(3,1) = 26
R( 4) = A(B( 4)) = A(B(0,1)) = A( 1) = A(1,0) =  8
R( 5) = A(B( 5)) = A(B(1,1)) = A( 4) = A(4,0) = 32
R( 6) = A(B( 6)) = A(B(2,1)) = A( 7) = A(1,1) = 10
R( 7) = A(B( 7)) = A(B(3,1)) = A(10) = A(4,1) = 34
R( 8) = A(B( 8)) = A(B(0,2)) = A( 2) = A(2,0) = 16
R( 9) = A(B( 9)) = A(B(1,2)) = A( 5) = A(5,0) = 40
R(10) = A(B(10)) = A(B(2,2)) = A( 8) = A(2,1) = 18
R(11) = A(B(11)) = A(B(3,2)) = A(11) = A(5,1) = 42

# 第idx个元素, 可以直接用下面的表达式计算
R = ((2,2),3):((24,2),8)

快速计算

TODO:

formula

  • let f: X->Y, g: Y->Z
  • g和f的composition: g o f: X->Z, (g o f)(x) = g(f(x))

impl

Complementation

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：http://github.com/66ring/2025/08/29/universe/gpu/cutlass_layout_algebra/

tags

评论